1. Un pilota vuole stabilire un nuovo record su un percorso di 50 km: percorrerlo alla velocità media di 100 km/h.
A causa di alcuni problemi tecnici impiega 40 minuti per percorrere i primi 25 km.
A quale velocità deve percorrere il resto del percorso (andando a velocità costante) per riuscire nel suo intento?
2. Quanti sono i numeri interi positivi multipli di almeno uno tra 5 e 7 e minori o uguali a 1000?
3. In un sacchetto ci sono 20 palline e su ciascuna è scritto un numero intero compreso tra 0 e 10 (0 e 10 inclusi). Il numero scritto su ogni pallina se non è zero è la somma dei numeri scritti su tutte le altre palline. Allora le palline su cui è scritto zero
sono:
4. 
La figura a fianco è la pianta di un quartiere, i punti A, B, C e D sono le case e i segmenti sono le strade. Da quante delle quattro case è possibile partire per fare un percorso che passi una e una sola volta da ogni strada (passando eventualmente più di una volta per una stessa casa)?
5. La somma di tutti i numeri naturali formati da due cifre distinte è:
6. 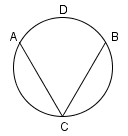
Il raggio della circonferenza a fianco è di
5 cm; inoltre i punti A, B e C dividono la circonferenza in tre archi di uguale lunghezza. Calcolare l'area delimitata dalle corde AC e BC e dall'arco di estremi A e B contenente D.
7. 
Le caselle di una scacchiera quadrata sono numerate come illustrato nella figura a fianco. Nella seconda colonna si trova la casella numero
38 e la casella della terza colonna che sta sulla sua stessa riga ha il numero
43. Quante caselle ha la scacchiera?
8. Ogni volta che Agilulfo torna a casa da scuola dopo aver preso un brutto voto, se la
sua mamma è in casa lo mette in punizione. Sapendo che ieri pomeriggio Agilulfo
non è stato messo in punizione, quale delle seguenti affermazioni è certamente vera?
9. La Polisportiva "I tropici" ha organizzato un torneo di calcio a cui partecipano 3 squadre ciascuna composta da 15 giocatori (riserve comprese) con maglie numerate da 1 a 15.
La notte prima delle partite ha nevicato e per poter giocare è necessario spalare la neve dal campo. Viene deciso allora di nominare un gruppo di 3 spalatori scegliendo un giocatore per squadra in modo che non ci siano due giocatori con lo stesso numero di maglia. In quanti modi diversi può essere formato il gruppo degli spalatori?
10. Su un foglio del quaderno di Carlo c'è un rettangolo con due lati gialli di 24 cm e due lati rossi di 36 cm. Carlo colora ogni punto del rettangolo dello stesso colore del lato più vicino al punto stesso. Quale sarà l'area della parte del rettangolo colorata di giallo?
11. C e T sono rispettivamente un cono e un cilindro circolari retti, che hanno lo stesso
asse e hanno le basi nello stesso piano (e sono rivolti dalla stessa parte rispetto a
questo piano). L'area di base di C misura 400π cm2 mentre il raggio di base di T misura 10 cm. Inoltre le altezze di C e T misurano entrambe 20 cm.
Quale percentuale del volume di C è contenuta dall'intersezione tra C e T?
12. Quante sono le terne ordinate distinte
(x, y, z) formate da numeri interi positivi (strettamente maggiori di zero) tali che
x2 + 2xy + y2 − z2 = 9?
13. Sia
N il più grande tra i numeri naturali
n che verificano la disuguaglianza
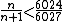
Qual è la somma delle cifre di
N?
14. La media aritmetica di ventisette numeri naturali consecutivi è 2008. Quanto vale il più piccolo tra essi?
15. Alberto, Barbara e Clara giocano in un grande piazzale dove ci sono 2008 birilli.
Alberto butta giù il triplo dei birilli buttati giù da Barbara, che a sua volta butta giù il doppio dei birilli buttati giù da Clara.
Quanti birilli al massimo può aver buttato giù Alberto?
16. Pietro e Paolo festeggiano il loro onomastico in pizzeria con i loro amici. Alla
fine della cena il conto viene diviso in parti uguali tra tutti i presenti e ciascuno
dovrebbe pagare 12 Euro. Con grande generosità però, gli amici decidono di offrire la cena a Pietro e Paolo; il conto viene nuovamente diviso in parti uguali tra gli amici di Pietro e Paolo (cioè tutti i presenti esclusi Pietro e Paolo), e ciascuno di loro paga 16 Euro. Quanti sono gli amici di Pietro e Paolo?
17. Su Marte, il Gran Ciambellano dell'Istruzione Marziana ha dichiarato che il prossimo anno scolastico ridurrà del 30% il numero dei maestri di scuola e che a coloro
che rimarranno in servizio lo stipendio sarà aumentato del 35%. La spesa complessiva per gli stipendi dei maestri quindi:
18. In un triangolo rettangolo ABC i cateti BC e CA misurano 7 cm e 24 cm rispettivamente. Sia H la proiezione di C sull'ipotenusa AB. Quanto vale il perimetro del triangolo HBC?
19. Per quanti valori distinti del numero reale
b l'equazione
x2 + bx − 16 = 0
ha due soluzioni reali (eventualmente coincidenti) e queste sono entrambe numeri
interi?
20. 
In un foglio a quadretti in cui il lato di un quadretto è
2 cm, sono disegnati due cerchi come nella figura a fianco. La misura della minima distanza tra i due
cerchi è:
21. Per ogni numero naturale
n, indichiamo con
Sn la somma dei primi dieci multipli di
n: ad esempio
S2 = 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20.
Quanto vale
S1 + S2 + S3 + . . . + S10?
22. Un quadrilatero ABCD ha le diagonali perpendicolari tra loro ed è inscritto in
una circonferenza c di diametro AC. L'area e il perimetro del quadrilatero sono
rispettivamente 48 cm2 e 28 cm. Quanto misura il raggio della circonferenza c?
23. Uno studente di Fibonacci inventò una sequenza di numeri definita in questo modo:
il primo e il secondo numero della sequenza sono 0 e 1 rispettivamente; ogni numero
della sequenza, dal terzo in poi, è pari alla somma di tutti i numeri che lo precedono (lui escluso!). Qual è il quindicesimo numero della sequenza?
24. n e
m sono due numeri interi positivi per cui:
![latex: \normalsize \sqrt[\small 3]{45+29\sqrt{2}}=m+n\sqrt{2}](https://www.diflo.it/test/cache/q0144/8d0dc5b3d4ba216b1ad3a3b7820e64af.gif )
. Quanto vale
n+m?
25. Giovanni vuole disegnare un quadrato formato da nove caselle (tre caselle per lato)
e scrivere in ogni casella un numero a scelta tra 0, 1, 2, 3, 4, in modo che fissata comunque una riga, una colonna o una diagonale del quadrato, la somma dei numeri presenti nelle sue caselle sia sempre uguale a 4. Quanti diversi quadrati può costruire?